2016년03월06일 63번

[사회통계]
구분되지 않는 n개의 공을 서로 다른 r개의 항아리에 넣는 방법의 수는? (단, r≤n이고 모든 항아리에는 최소한 1개 이상의 공이 들어가야 한다.)

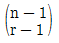
(정답률: 38%)

문제 해설

이 문제는 볼프강 암데르먼(Wolfgang Amadeus Amdeurman)의 볼프강 암데르먼의 증명을 이용하면 간단하게 해결할 수 있다.

우선 모든 공을 일렬로 늘어놓고, 이 중에서 r-1개의 구분선을 선택하여 공을 r개의 그룹으로 나눈다. 이때, 각 그룹에는 최소한 1개의 공이 들어가야 하므로, 각 구분선은 적어도 하나의 공을 가지고 있어야 한다.

따라서, 구분선을 선택하는 방법의 수는 (n-1) C (r-1)이 된다. (n-1) C (r-1)은 n-1개의 원소 중에서 r-1개를 선택하는 조합의 수를 의미한다.

그리고 각 그룹에는 구분선을 제외한 나머지 공들이 들어가게 되므로, 각 그룹에 들어갈 공의 수는 n-r이 된다.

따라서, 전체 방법의 수는 (n-1) C (r-1) * (n-r)^(r-1)이 된다.

위의 보기 중에서 "

"가 정답인 이유는 이 공식이다.

이전 문제 다음 문제